Los modelos de aprendizaje profundo, como las redes neuronales, construyen representaciones abstractas de los datos durante la fase de entrenamiento. En esta etapa, el objetivo es optimizar una función de costo, ya sea minimizándola o maximizándola, mediante algoritmos como los de la familia del gradiente descendente.

En las redes neuronales, este proceso se aplica a cada una de las capas del modelo. Así, cada capa aprende una representación específica de los datos. Dado que las capas están conectadas entre sí, se forma una estructura jerárquica: las capas más profundas —aquellas más cercanas a la salida— capturan patrones complejos generados por las capas anteriores.

Un aspecto particularmente interesante es entender cómo se estructura la información en estas capas profundas. Esta es un área de investigación activa, ya que las redes neuronales profundas suelen tratarse como cajas negras (black boxes).

Durante el desarrollo de nuestra tesis de maestría en Ciencia de Datos, nos enfrentamos a este desafío. Diseñamos un modelo de deep learning que combinaba información de imágenes y series de tiempo, utilizando una red convolucional y una red convolucional temporal. Este modelo se aplicó a un problema de clasificación binaria.

Con el objetivo de analizar cómo influía la incorporación progresiva de información en la toma de decisiones del modelo, seleccionamos una variable de interés denominada \(\text{Seq}\), distribuida en cinco columnas: \(\text{Seq}_1, \text{Seq}_2, \ldots, \text{Seq}_5\).

Seleccionamos una muestra representativa de ambas clases y la ingresamos al modelo, registrando las activaciones generadas en la penúltima capa para cada iteración, a medida que se agregaban progresivamente las variables \(\text{Seq}_i\).

Esto nos permitió construir una matriz de activaciones:

$$
M \in \mathbb{R}^{m \times n}
$$

donde \(m\) representa el número de muestras seleccionadas y \(n\) el número de neuronas en la penúltima capa.

Dado que \(M\) es de alta dimensionalidad, fue necesario aplicar técnicas de reducción de dimensiones para visualizar las representaciones aprendidas. El objetivo era proyectar \(M\) en un nuevo espacio de dimensión \(k\), tal que \(k < n \):

$$
M’ = f(M), \quad M’ \in \mathbb{R}^{m \times k}
$$

Para esta tarea, utilizamos dos algoritmos ampliamente conocidos:

Análisis de Componentes Principales (PCA)

PCA transforma los datos mediante combinaciones lineales ortogonales que maximizan la varianza. Matemáticamente, busca una matriz de proyección \(W\) tal que:

$$
M’ = M W
$$

donde las columnas de \(W\) son los vectores propios de la matriz de covarianza de \(M\), asociados a los mayores valores propios.

Uniform Manifold Approximation and Projection (UMAP)

UMAP es una técnica no lineal que preserva tanto la estructura local como global de los datos. A diferencia de PCA, UMAP construye un grafo de proximidad en el espacio de alta dimensión y lo proyecta en un espacio de menor dimensión, optimizando la preservación de la topología. Aunque su formulación matemática es más compleja, se basa en minimizar la divergencia entre distribuciones de probabilidad en ambos espacios

Visualización

Para la visualización, decidimos considerar un espacio reducido de dimensión \(k = 2\). Iteramos de manera incremental por las variables \(\text{Seq}_1\) hasta \(\text{Seq}_5\), capturando las activaciones correspondientes en cada paso.

Los resultados obtenidos al aplicar PCA se muestran a continuación:

Como se puede observar, a medida que se incrementa el número de variables, la separación entre clases se vuelve más evidente. Además, se aprecia que la estructura del espacio de clases se transforma progresivamente, siendo con \(\text{Seq}_5\) más diferenciable y clara la separación entre las clases.

Este comportamiento también se manifiesta al aplicar UMAP:

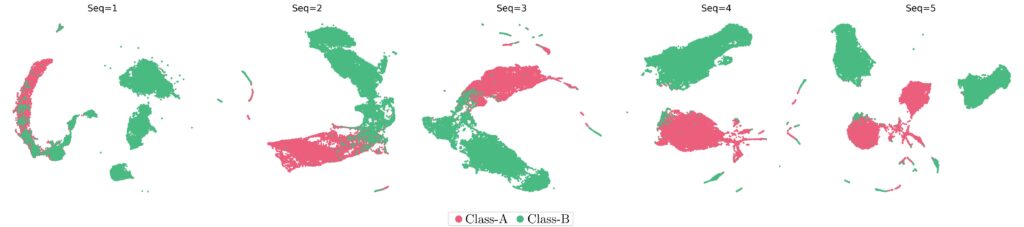
En estas visualizaciones, se aprecia cómo las clases se separan con mayor claridad conforme se incorpora más información de la variable \(\text{Seq}\). Al comparar ambas técnicas, notamos que el modelo mejora su capacidad de diferenciación entre clases a medida que se enriquece la entrada de datos.

Contar con dos enfoques de visualización nos permite evaluar la relevancia de la variable \(\text{Seq}\) desde perspectivas complementarias: PCA desde una visión lineal y global, y UMAP desde una perspectiva no lineal que preserva la topología local.

Finalmente, para observar de forma más dinámica cómo se transforma el espacio de representaciones, decidimos crear una animación utilizando las visualizaciones obtenidas con UMAP. El resultado se muestra a continuación:

Conclusiones

Este estudio nos permitió explorar cómo las representaciones internas de un modelo de deep learning evolucionan al incorporar progresivamente información relevante. A través de técnicas de reducción de dimensiones como PCA y UMAP, logramos visualizar cómo se estructura el espacio de clases en la penúltima capa del modelo.

Los resultados muestran que:

• La incorporación incremental de variables mejora la diferenciación entre clases.
• PCA y UMAP ofrecen perspectivas complementarias para analizar la estructura de los datos.
• La variable \(\text{Seq}\) tiene un impacto significativo en la capacidad del modelo para discriminar entre clases.

Estas visualizaciones no solo enriquecen el análisis técnico, sino que también aportan interpretabilidad a modelos que tradicionalmente se consideran cajas negras. En futuras investigaciones, este enfoque podría extenderse a otros tipos de variables y arquitecturas, contribuyendo a una comprensión más profunda del aprendizaje representacional en redes neuronales.